Wzór trapezów

Wzór trapezów – jeden z wielu wzorów służących do przybliżonego obliczania całek oznaczonych w sensie Riemanna. Idea wzoru opiera się na geometrycznej interpretacji całki oznaczonej z funkcji nieujemnej jako pola pod wykresem funkcji.

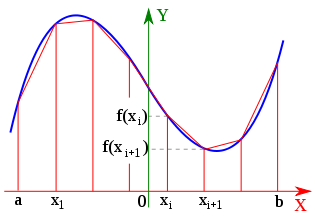
Jeżeli przedział całkowania [a, b] podzielony zostanie punktami x₁, x₂, ..., x_n-1 na n równych części o długościach (b-a)/n, i w figurę ograniczoną na prostymi x = a, x = b, osią odciętych oraz wykresem funkcji y = f(x) wpiszemy trapezy jak pokazano na rysunku poniżej,

to pola kolejnych trapezów wynoszą:

gdzie dla jednolitości oznaczono a = x₀ i b = x_n.

Suma pól trapezów jest w przybliżeniu równa polu całego obszaru, czyli:

.

Ten właśnie wzór nazywany jest wzorem trapezów.

W przypadku funkcji ciągłej na przedziale [a, b], wzór trapezów pozwala obliczać jej całkę oznaczoną na tym przedziale z dowolną dokładnością, wystarczy w tym celu wziąć za n odpowiednio dużą liczbę. Błąd przybliżenia daje się oszacować w przypadku funkcji, która ma na przedziale [a, b] ciągłą drugą pochodną:

gdzie K oznacza największą wartość funkcji |f ′′(x)| w przedziale [a, b].

Obecnie wzór trapezów ma znaczenie wyłącznie historyczne – dostępne programy do całkowania numerycznego stosują o wiele dokładniejsze metody i pozwalają uniknąć czasochłonnych rachunków.