Kwadraturami Gaussa nazywamy metody całkowania numerycznego polegające na takim wyborze wag  i węzłów interpolacji
i węzłów interpolacji ![t_1, t_2, \ldots, t_n \in [a,b]](https://upload.wikimedia.org/math/a/e/1/ae1c9f6951bd62c10e063db2033c6973.png) aby wyrażenie
aby wyrażenie
 i węzłów interpolacji
i węzłów interpolacji ![t_1, t_2, \ldots, t_n \in [a,b]](https://upload.wikimedia.org/math/a/e/1/ae1c9f6951bd62c10e063db2033c6973.png) aby wyrażenie
aby wyrażenie
najlepiej przybliżało całkę
 ,
, jest skończona,
jest skończona,- Jeżeli
 jest wielomianem takim, że
jest wielomianem takim, że ![\forall_{x\in [a,b]}\;p(x)\ge 0](https://upload.wikimedia.org/math/7/d/2/7d24afd04dc7bc7d989ae05ec964b18b.png) , to jeśli
, to jeśli  , mamy wtedy
, mamy wtedy  .
.
Określmy iloczyn skalarny z wagą
Powiemy, że dwa wielomiany są ortogonalne względem tego iloczynu skalarnego jeśli  .
.
 .
.
Wszystkie kwadratury Gaussa wywodzą się z twierdzenia udowodnionego przez niego:
to dla każdego wielomianu  stopnia nie większego niż 2n-1 zachodzi
stopnia nie większego niż 2n-1 zachodzi
 stopnia nie większego niż 2n-1 zachodzi
stopnia nie większego niż 2n-1 zachodzi
Ponadto  .
.
 .
.
b) Jeżeli dla pewnego ciągu węzłów ![x_1, x_2, \ldots, x_n \in [a,b]](https://upload.wikimedia.org/math/6/4/8/648948a79d683e06f2356c346cead9b5.png) oraz ciągu wag
oraz ciągu wag 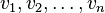 dla dowolnego wielomianu
dla dowolnego wielomianu  stopnia nie większego niż 2n-1 zachodzi warunek (*), to
stopnia nie większego niż 2n-1 zachodzi warunek (*), to  oraz
oraz  z dokładnością do kolejności.
z dokładnością do kolejności.
![x_1, x_2, \ldots, x_n \in [a,b]](https://upload.wikimedia.org/math/6/4/8/648948a79d683e06f2356c346cead9b5.png) oraz ciągu wag
oraz ciągu wag 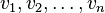 dla dowolnego wielomianu
dla dowolnego wielomianu  stopnia nie większego niż 2n-1 zachodzi warunek (*), to
stopnia nie większego niż 2n-1 zachodzi warunek (*), to  oraz
oraz  z dokładnością do kolejności.
z dokładnością do kolejności.
c) Dla dowolnego ciągu węzłów ![x_1, x_2, \ldots, x_n \in [a,b]](https://upload.wikimedia.org/math/6/4/8/648948a79d683e06f2356c346cead9b5.png) oraz ciągu wag
oraz ciągu wag 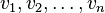 nie istnieje wielomian stopnia 2n, dla którego nie zachodzi warunek (*).
nie istnieje wielomian stopnia 2n, dla którego nie zachodzi warunek (*).
![x_1, x_2, \ldots, x_n \in [a,b]](https://upload.wikimedia.org/math/6/4/8/648948a79d683e06f2356c346cead9b5.png) oraz ciągu wag
oraz ciągu wag 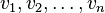 nie istnieje wielomian stopnia 2n, dla którego nie zachodzi warunek (*).
nie istnieje wielomian stopnia 2n, dla którego nie zachodzi warunek (*).

 jest dowolną
jest dowolną ![[a,b]](https://upload.wikimedia.org/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) , a
, a  jest tzw. funkcją wagową spełniającą warunki
jest tzw. funkcją wagową spełniającą warunki
 oraz
oraz 

Brak komentarzy:
Prześlij komentarz