Metody numeryczne: Fourier

Szybka transformacja Fouriera (ang. FFT od Fast Fourier Transform) to algorytm liczenia dyskretnej transformaty Fouriera oraz transformaty do niej odwrotnej.

Czasem używana jest też forma szybka transformata Fouriera w odniesieniu do tej metody. Ściśle jednak transformacja jest przekształceniem, a transformata wynikiem tego przekształcenia.

Niech x₀, ...., x_N-1 będą liczbami zespolonymi, wtedy dyskretna transformata Fouriera jest określona wzorem

$X_k = \sum_{n=0}^{N-1} x_n e^{-{2\pi i \over N} nk } \qquad k = 0,\dots,N-1.$

Obliczanie tych sum za pomocą powyższego wzoru zajęłoby O(N²) operacji.

Algorytmy (jak algorytm Cooleya-Tukeya) obliczające szybką transformację Fouriera bazują na metodzie dziel i zwyciężaj rekurencyjnie dzieląc transformatę wielkości N = N₁N₂ na transformaty wielkości N₁ i N₂ z wykorzystaniem O(N) operacji mnożenia.

Najpopularniejszą wersją FFT jest FFT o podstawie 2. Jest to bardzo efektywna operacja, jednak wektor próbek wejściowych (spróbkowany sygnał) musi mieć długość $N=2^k$ , gdzie $k$ to pewna liczba naturalna. Wynik otrzymuje się na drodze schematycznych przekształceń, opartych o tak zwane struktury motylkowe.

Złożoność obliczeniowa Szybkiej transformacji Fouriera wynosi $O(N \log_2 N)$ , zamiast $O(N^2)$ algorytmu wynikającego wprost ze wzoru określającego dyskretną transformatę Fouriera. Dzięki istnieniu takiego algorytmu praktycznie możliwe stało się cyfrowe przetwarzanie sygnałów (DSP), a także zastosowanie dyskretnych transformat kosinusowych (DCT) (JPEG,MP3 itd.) do kompresji.

Metody numeryczne

piątek, 17 stycznia 2014

Fourier

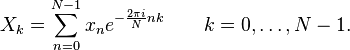
Brak komentarzy:

Prześlij komentarz