Kwadraturami Gaussa nazywamy metody całkowania numerycznego polegające na takim wyborze wag  i węzłów interpolacji
i węzłów interpolacji ![t_1, t_2, \ldots, t_n \in [a,b]](https://upload.wikimedia.org/math/a/e/1/ae1c9f6951bd62c10e063db2033c6973.png) aby wyrażenie
aby wyrażenie
 i węzłów interpolacji
i węzłów interpolacji ![t_1, t_2, \ldots, t_n \in [a,b]](https://upload.wikimedia.org/math/a/e/1/ae1c9f6951bd62c10e063db2033c6973.png) aby wyrażenie
aby wyrażenie
najlepiej przybliżało całkę
 ,
, jest skończona,
jest skończona,- Jeżeli
 jest wielomianem takim, że
jest wielomianem takim, że ![\forall_{x\in [a,b]}\;p(x)\ge 0](https://upload.wikimedia.org/math/7/d/2/7d24afd04dc7bc7d989ae05ec964b18b.png) , to jeśli
, to jeśli  , mamy wtedy
, mamy wtedy  .
.
Określmy iloczyn skalarny z wagą
Powiemy, że dwa wielomiany są ortogonalne względem tego iloczynu skalarnego jeśli  .
.
 .
.
Wszystkie kwadratury Gaussa wywodzą się z twierdzenia udowodnionego przez niego:
to dla każdego wielomianu  stopnia nie większego niż 2n-1 zachodzi
stopnia nie większego niż 2n-1 zachodzi
 stopnia nie większego niż 2n-1 zachodzi
stopnia nie większego niż 2n-1 zachodzi
Ponadto  .
.
 .
.
b) Jeżeli dla pewnego ciągu węzłów ![x_1, x_2, \ldots, x_n \in [a,b]](https://upload.wikimedia.org/math/6/4/8/648948a79d683e06f2356c346cead9b5.png) oraz ciągu wag
oraz ciągu wag 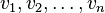 dla dowolnego wielomianu
dla dowolnego wielomianu  stopnia nie większego niż 2n-1 zachodzi warunek (*), to
stopnia nie większego niż 2n-1 zachodzi warunek (*), to  oraz
oraz  z dokładnością do kolejności.
z dokładnością do kolejności.
![x_1, x_2, \ldots, x_n \in [a,b]](https://upload.wikimedia.org/math/6/4/8/648948a79d683e06f2356c346cead9b5.png) oraz ciągu wag
oraz ciągu wag 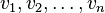 dla dowolnego wielomianu
dla dowolnego wielomianu  stopnia nie większego niż 2n-1 zachodzi warunek (*), to
stopnia nie większego niż 2n-1 zachodzi warunek (*), to  oraz
oraz  z dokładnością do kolejności.
z dokładnością do kolejności.
c) Dla dowolnego ciągu węzłów ![x_1, x_2, \ldots, x_n \in [a,b]](https://upload.wikimedia.org/math/6/4/8/648948a79d683e06f2356c346cead9b5.png) oraz ciągu wag
oraz ciągu wag 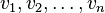 nie istnieje wielomian stopnia 2n, dla którego nie zachodzi warunek (*).
nie istnieje wielomian stopnia 2n, dla którego nie zachodzi warunek (*).
![x_1, x_2, \ldots, x_n \in [a,b]](https://upload.wikimedia.org/math/6/4/8/648948a79d683e06f2356c346cead9b5.png) oraz ciągu wag
oraz ciągu wag 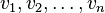 nie istnieje wielomian stopnia 2n, dla którego nie zachodzi warunek (*).
nie istnieje wielomian stopnia 2n, dla którego nie zachodzi warunek (*).

 jest dowolną
jest dowolną ![[a,b]](https://upload.wikimedia.org/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) , a
, a  jest tzw. funkcją wagową spełniającą warunki
jest tzw. funkcją wagową spełniającą warunki
 oraz
oraz 


 .
.
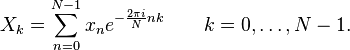
 , gdzie
, gdzie  to pewna liczba naturalna. Wynik otrzymuje się na drodze schematycznych przekształceń, opartych o tak zwane struktury motylkowe.
to pewna liczba naturalna. Wynik otrzymuje się na drodze schematycznych przekształceń, opartych o tak zwane struktury motylkowe. , zamiast
, zamiast  algorytmu wynikającego wprost ze wzoru określającego
algorytmu wynikającego wprost ze wzoru określającego 

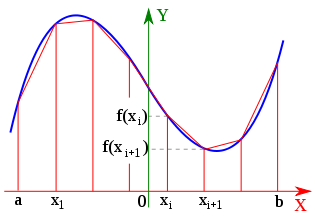
 są równo odległymi węzłami interpolacji funkcji f(x) (tj.
są równo odległymi węzłami interpolacji funkcji f(x) (tj.  są elementami dziedziny f, dla których znana jest wartość
są elementami dziedziny f, dla których znana jest wartość  ), to całkę:
), to całkę:

 jest
jest 
 oznacza długość kroku dzielącą dwa węzły interpolacji.
oznacza długość kroku dzielącą dwa węzły interpolacji.


 ,
,

 t=0
t=0 t=1
t=1
 t=n
t=n



 (nazywane współczynnikami kwadratury Newtona-Cotesa), otrzymuje się:
(nazywane współczynnikami kwadratury Newtona-Cotesa), otrzymuje się:

 .
.


 .
.

