Metody numeryczne

czwartek, 24 kwietnia 2014

p04

package p04;

import java.awt.Color;
import java.awt.Component;
import java.awt.Font;
import java.awt.Frame;
import java.awt.Graphics;
import java.awt.Menu;
import java.awt.MenuBar;
import java.awt.MenuItem;
import java.awt.event.ActionEvent;
import java.awt.event.ActionListener;
import java.awt.event.MouseListener;
import java.awt.event.WindowEvent;
import java.awt.event.WindowListener;

import javax.swing.Timer;

import org.w3c.dom.events.MouseEvent;

public class Startowa extends Frame implements WindowListener {

/**
*
*/
private static final long serialVersionUID = 6308864627364406090L;
private int licznik=0;
private Timer timer;

public Startowa(String string) {
// TODO Auto-generated constructor stub
super(string);
timer=new Timer(1000, new ActionListener(){

@Override
public void actionPerformed(ActionEvent e) {
// TODO Auto-generated method stub
licznik++;
repaint();
}

});
timer.start();
setSize(400,300);
addWindowListener(this );
addMouseListener(new MouseListener(){

@Override
public void mouseClicked(java.awt.event.MouseEvent e) {
// TODO Auto-generated method stub
if(timer.isRunning()) timer.stop();
else timer.start();
}

@Override
public void mousePressed(java.awt.event.MouseEvent e) {
// TODO Auto-generated method stub

}

@Override
public void mouseReleased(java.awt.event.MouseEvent e) {
// TODO Auto-generated method stub

}

@Override
public void mouseEntered(java.awt.event.MouseEvent e) {
// TODO Auto-generated method stub

}

@Override
public void mouseExited(java.awt.event.MouseEvent e) {
// TODO Auto-generated method stub

}

});

MenuBar mb= new MenuBar();
Menu m1= new Menu("Pliki");
MenuItem mi1=new MenuItem("Start");
MenuItem mi2=new MenuItem("Stop");
MenuItem mi3=new MenuItem("Koniec");

m1.add(mi1);
m1.add(mi2);
m1.add(mi3);
mb.add(m1);
setMenuBar(mb);
m1.addActionListener(new ActionListener(){

@Override
public void actionPerformed(ActionEvent e) {
// TODO Auto-generated method stub
switch(e.getActionCommand()){
case"Start":timer.start();break;

case "Stop":timer.stop(); break;

case "Koniec":System.exit(0);break;

}
}

});

setVisible(true);

}

public void paint(Graphics g){
g.setColor(new Color(0,0,0));
g.setFont(g.getFont().deriveFont(24.0f).deriveFont(Font.ITALIC));
g.drawString("Licznik="+licznik, 100, 100);

}

private void drawString(String string, int i, int j) {
// TODO Auto-generated method stub

}

@Override
public void windowOpened(WindowEvent e) {
// TODO Auto-generated method stub

}

@Override
public void windowClosing(WindowEvent e) {
// TODO Auto-generated method stub
System.exit(0);
}

@Override
public void windowClosed(WindowEvent e) {
// TODO Auto-generated method stub

}

@Override
public void windowIconified(WindowEvent e) {
// TODO Auto-generated method stub

}

@Override
public void windowDeiconified(WindowEvent e) {
// TODO Auto-generated method stub

}

@Override
public void windowActivated(WindowEvent e) {
// TODO Auto-generated method stub

}

@Override
public void windowDeactivated(WindowEvent e) {
// TODO Auto-generated method stub

}

public static void main(String[] args) {
// TODO Auto-generated method stub
new Startowa("Moje okienko");

}

}

napisac cos z ruchami myszki

startowa.java

package p02;

import java.util.Arrays;
import java.util.Random;

public class Startowa extends Object{
public class Wewnetrzna{
public void Wypisz(){
System.out.println("Klasa Wewnetrzna");
}

}

public static class WewStatyczna{
public void Wypisz(){
System.out.println("Klasa Wewnetrzna i statyczna");

}}
public static void main(String[] args) {
int [] tab= new int [10];
Random r = new Random();
for (int i=0;i<10;i++)
tab[i]=r.nextInt(100);
for(int x:tab)
System.out.println(x);
Arrays.sort(tab);
System.out.println(Arrays.toString(tab));
Klasa k=new Klasa();
k.Wypisz();
Wewnetrzna w=new Startowa().new Wewnetrzna();
w.Wypisz();
WewStatyczna ws = new WewStatyczna();
ws.Wypisz();
new myinterface(){
@Override
public void Wypisz(){

System.out.println("Anonimowa");
}

}.Wypisz();;
class Lokalna implements myinterface{
@Override
public void Wypisz(){
System.out.println("Lokalna");
}
}

Lokalna l=new Lokalna();
l.Wypisz();

}

}

Klasa.java

package p02;

public class Klasa implements myinterface{

@Override

public void Wypisz(){

System.out.println("klasa z interfejsem");

}

http://docs.oracle.com/javase/specs/index.html

pierwszy program

package pierwsza;

import java.util.*;

public class Pierwsza {

public static void main(String[] args) {

Scanner sc=new Scanner(System.in);

Random r = new Random();

//int [] tab=new int [1];

//for (int i=0;i<10;i++)

// tab[i]=r.nextInt(100);

int x=r.nextInt(100);

for (int i=0;i<5;i++){

int y=sc.nextInt();

if (y<x) System.out.println("za nisko");

if (x<y) System.out.println("za wysoko");

if (x==y) System.out.println("Trafiles!"); break;

}

System.out.println("Poszukiwana liczba to:");

System.out.println(x);

}}

piątek, 17 stycznia 2014

Kwadratura Gaussa

Kwadraturami Gaussa nazywamy metody całkowania numerycznego polegające na takim wyborze wag $w_1, w_2, \ldots, w_n$ i węzłów interpolacji $t_1, t_2, \ldots, t_n \in [a,b]$ aby wyrażenie

$\sum_{i=1}^n w_i f(t_i)$

najlepiej przybliżało całkę

$I(f) = \int\limits_a^b w(x) f(x) dx$

gdzie $f$ jest dowolną funkcją określoną na odcinku $[a,b]$ , a $w$ jest tzw. funkcją wagową spełniającą warunki

$w(x)\ge 0$ ,
$\forall_{k\in \mathbb{N}} \int\limits_a^b x^k w(x) dx$ jest skończona,
Jeżeli $p$ jest wielomianem takim, że $\forall_{x\in [a,b]}\;p(x)\ge 0$ , to jeśli $\int\limits_a^b w(x) p(x) dx=0$ , mamy wtedy $p\equiv0$ .

Określmy iloczyn skalarny z wagą

$\langle f,g \rangle_w = \int\limits_a^b w(x) f(x) g(x) dx.$

Powiemy, że dwa wielomiany są ortogonalne względem tego iloczynu skalarnego jeśli $\langle f,g \rangle_w =0$ .

Wszystkie kwadratury Gaussa wywodzą się z twierdzenia udowodnionego przez niego:

a) Jeżeli $t_1, t_2, \ldots, t_n \in [a,b]$ są pierwiastkami n-tego wielomianu ortogonalnego $p_n(x)$ oraz $w_1, w_2, \ldots, w_n$ są rozwiązaniami układu równań:

$\left\{ \begin{matrix} p_0(t_1)w_1 + & \ldots & + p_0(t_n)w_n= & <p_0,p_0>_w\\ p_1(t_1)w_1 + & \ldots & + p_1(t_n)w_n= & 0\\ \vdots & & \vdots & \vdots \\ p_{n-1}(t_1)w_1 + & \ldots & + p_{n-1}(t_n)w_n= & 0\\ \end{matrix}\right.$

to dla każdego wielomianu $p$ stopnia nie większego niż 2n-1 zachodzi

$\int\limits_a^b w(x) p(x) dx = \sum_{i=1}^n w_i p(t_i).\qquad (*)$

Ponadto $w_i > 0$ .

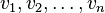b) Jeżeli dla pewnego ciągu węzłów $x_1, x_2, \ldots, x_n \in [a,b]$ oraz ciągu wag $v_1, v_2, \ldots, v_n$ dla dowolnego wielomianu $p$ stopnia nie większego niż 2n-1 zachodzi warunek (*), to $x_i=t_i$ oraz $v_i=w_i$ z dokładnością do kolejności.

c) Dla dowolnego ciągu węzłów $x_1, x_2, \ldots, x_n \in [a,b]$ oraz ciągu wag $v_1, v_2, \ldots, v_n$ nie istnieje wielomian stopnia 2n, dla którego nie zachodzi warunek (*).

Wzór trapezów

Wzór trapezów – jeden z wielu wzorów służących do przybliżonego obliczania całek oznaczonych w sensie Riemanna. Idea wzoru opiera się na geometrycznej interpretacji całki oznaczonej z funkcji nieujemnej jako pola pod wykresem funkcji.

Jeżeli przedział całkowania [a, b] podzielony zostanie punktami x₁, x₂, ..., x_n-1 na n równych części o długościach (b-a)/n, i w figurę ograniczoną na prostymi x = a, x = b, osią odciętych oraz wykresem funkcji y = f(x) wpiszemy trapezy jak pokazano na rysunku poniżej,

to pola kolejnych trapezów wynoszą:

$\frac{b-a}{n}\cdot\frac{f(x_0)+f(x_1)}{2},\ \frac{b-a}{n}\cdot\frac{f(x_1)+f(x_2)}{2},\ \dots, \frac{b-a}{n}\cdot\frac{f(x_{n-1})+f(x_n)}{2}$

gdzie dla jednolitości oznaczono a = x₀ i b = x_n.

Suma pól trapezów jest w przybliżeniu równa polu całego obszaru, czyli:

$\int\limits_a^b f(x)\,dx\approx\frac{b-a}{{2}{n}}\left(f(x_0)+f(x_n)+2f(x_1)+\dots+2f(x_{n-1})\right)$ .

Ten właśnie wzór nazywany jest wzorem trapezów.

W przypadku funkcji ciągłej na przedziale [a, b], wzór trapezów pozwala obliczać jej całkę oznaczoną na tym przedziale z dowolną dokładnością, wystarczy w tym celu wziąć za n odpowiednio dużą liczbę. Błąd przybliżenia daje się oszacować w przypadku funkcji, która ma na przedziale [a, b] ciągłą drugą pochodną:

$|R_n|\le\left|\frac{(b-a)^3}{12n^2}K\right|$

gdzie K oznacza największą wartość funkcji |f ′′(x)| w przedziale [a, b].

Obecnie wzór trapezów ma znaczenie wyłącznie historyczne – dostępne programy do całkowania numerycznego stosują o wiele dokładniejsze metody i pozwalają uniknąć czasochłonnych rachunków.

Fourier

Szybka transformacja Fouriera (ang. FFT od Fast Fourier Transform) to algorytm liczenia dyskretnej transformaty Fouriera oraz transformaty do niej odwrotnej.

Czasem używana jest też forma szybka transformata Fouriera w odniesieniu do tej metody. Ściśle jednak transformacja jest przekształceniem, a transformata wynikiem tego przekształcenia.

Niech x₀, ...., x_N-1 będą liczbami zespolonymi, wtedy dyskretna transformata Fouriera jest określona wzorem

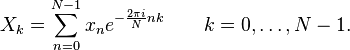
$X_k = \sum_{n=0}^{N-1} x_n e^{-{2\pi i \over N} nk } \qquad k = 0,\dots,N-1.$

Obliczanie tych sum za pomocą powyższego wzoru zajęłoby O(N²) operacji.

Algorytmy (jak algorytm Cooleya-Tukeya) obliczające szybką transformację Fouriera bazują na metodzie dziel i zwyciężaj rekurencyjnie dzieląc transformatę wielkości N = N₁N₂ na transformaty wielkości N₁ i N₂ z wykorzystaniem O(N) operacji mnożenia.

Najpopularniejszą wersją FFT jest FFT o podstawie 2. Jest to bardzo efektywna operacja, jednak wektor próbek wejściowych (spróbkowany sygnał) musi mieć długość $N=2^k$ , gdzie $k$ to pewna liczba naturalna. Wynik otrzymuje się na drodze schematycznych przekształceń, opartych o tak zwane struktury motylkowe.

Złożoność obliczeniowa Szybkiej transformacji Fouriera wynosi $O(N \log_2 N)$ , zamiast $O(N^2)$ algorytmu wynikającego wprost ze wzoru określającego dyskretną transformatę Fouriera. Dzięki istnieniu takiego algorytmu praktycznie możliwe stało się cyfrowe przetwarzanie sygnałów (DSP), a także zastosowanie dyskretnych transformat kosinusowych (DCT) (JPEG,MP3 itd.) do kompresji.

Monte Carlo

Metoda Monte Carlo (MC) jest stosowana do modelowania matematycznego procesów zbyt złożonych (obliczania całek, łańcuchów procesów statystycznych), aby można było przewidzieć ich wyniki za pomocą podejścia analitycznego. Istotną rolę w metodzie MC odgrywa losowanie (wybór przypadkowy) wielkości charakteryzujących proces, przy czym losowanie dokonywane jest zgodnie z rozkładem, który musi być znany.

Typowym przykładem może być modelowanie wyniku zderzenia cząstki o wysokiej energii z jądrem złożonym, gdzie każdy akt zderzenia elementarnego (z pojedynczym nukleonem jądra) modelowany jest oddzielnie poprzez losowanie liczby, rodzaju, kąta emisji, energii itp. cząstek wtórnych emitowanych w wyniku takiego zderzenia. Następnym etapem jest modelowanie losu każdej z cząstek wtórnych (w wyniku kolejnego losowania prawdopodobieństwa oddziaływania lub wyjścia z jądra). Kontynuując taką procedurę można otrzymać pełny opis "sztucznie generowanego" procesu złożonego. Po zebraniu dostatecznie dużej liczby takich informacji można zestawić ich charakterystyki z obserwowanymi wynikami doświadczalnymi, potwierdzając lub negując słuszność poczynionych w całej procedurze założeń.

Metoda została opracowana i pierwszy raz zastosowana przez Stanisława Ulama.

Metodą Monte Carlo można obliczyć pole figury zdefiniowanej nierównością:

$x^2 +y^2 \le R^2$

czyli koła o promieniu R i środku w punkcie (0,0).

Losuje się n punktów z opisanego na tym kole kwadratu - dla koła o R = 1 współrzędne wierzchołków (-1,-1), (-1,1), (1,1), (1,-1).
Po wylosowaniu każdego z tych punktów trzeba sprawdzić, czy jego współrzędne spełniają powyższą nierówność (tj. czy punkt należy do koła).

Wynikiem losowania jest informacja, że z n wszystkich prób k było trafionych, zatem pole koła wynosi

$P_k=P\ \frac {k}{n}$

gdzie P jest polem kwadratu opisanego na kole (Dla R = 1 : P = 4).