Interpolacja jest często stosowana w naukach doświadczalnych, gdzie dysponuje się zazwyczaj skończoną liczbą danych do określenia zależności między wielkościami.
Zgodnie z
twierdzeniem Weierstrassa dowolną funkcję
y=f(x) ciągłą na przedziale domkniętym można dowolnie przybliżyć za pomocą wielomianu odpowiednio wysokiego stopnia.
Ogólna metoda

Przykład interpolacji wielomianowej.
Metoda interpolacji polega na:
- wybraniu
 punktów
punktów  należących do dziedziny
należących do dziedziny  , dla których znane są wartości
, dla których znane są wartości 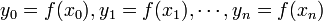
- znalezieniu wielomianu
 stopnia co najwyżej
stopnia co najwyżej  takiego, że
takiego, że 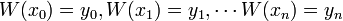 .
.
Interpretacja geometryczna – dla danych

punktów na wykresie szuka się wielomianu stopnia co najwyżej

, którego wykres przechodzi przez dane punkty
Znajdowanie odpowiedniego wielomianu[edytuj | edytuj kod]
Wielomian przyjmujący zadane wartości w konkretnych punktach można zbudować w ten sposób:
- Dla pierwszego węzła o wartości
 znajduje się wielomian, który w tym punkcie przyjmuje wartość
znajduje się wielomian, który w tym punkcie przyjmuje wartość  , a w pozostałych węzłach
, a w pozostałych węzłach  wartość zero.
wartość zero.
- Dla kolejnego węzła znajduje sie podobny wielomian, który w drugim węźle przyjmuje wartość
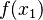 , a w pozostałych węzłach
, a w pozostałych węzłach  wartość zero.
wartość zero.
- Dodaje się wartość ostatnio obliczonego wielomianu do wartości poprzedniego
- Dla każdego z pozostałych węzłów znajduje się podobny wielomian, za każdym razem dodając go do wielomianu wynikowego
- Wielomian będący sumą wielomianów obliczonych dla poszczególnych węzłów jest wielomianem interpolującym
Dowód ostatniego punktu i dokładny sposób tworzenia poszczególnych wielomianów opisany jest poniżej w dowodzie istnienia wielomianu interpolującego będącego podstawą algorytmu odnajdowania tego wielomianu.
Dowód istnienia wielomianu interpolującego
Niech

będą węzłami interpolacji funkcji
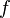
takimi, że znane są wartości

Można zdefiniować funkcję:
 ,
, 
taką, że dla


jest
wielomianem stopnia

(mianownik jest liczbą, a licznik iloczynem

wyrazów postaci

)
- Gdy
 i
i  :
:

- Gdy
 i
i  :
:

(licznik = 0 ponieważ występuje element

)
Niech

będzie wielomianem stopnia co najwyżej

, określonym jako:

Dla

 .
.
Wszystkie składniki sumy o indeksach różnych od

są równe zeru (ponieważ dla

, składnik o indeksie

jest równy:
 .
.
A więc

z czego wynika, że

jest wielomianem interpolującym funkcję

w punktach

.
ma na końcach przedziału domkniętego wartości różnych znaków, to wewnątrz tego przedziału, istnieje co najmniej jeden pierwiastek równania
 jest ciągła w przedziale domkniętym
jest ciągła w przedziale domkniętym ![[a;b]](http://upload.wikimedia.org/math/9/4/a/94acf62f087ab3268b2b3fa5a8a7a79c.png)

 czyli czy
czyli czy 
 dzieli przedział
dzieli przedział ![[a,b]](http://upload.wikimedia.org/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) na dwa mniejsze przedziały
na dwa mniejsze przedziały ![[a, x_1]](http://upload.wikimedia.org/math/5/4/2/5429f4c0251caaaaae7db85bd1503f57.png) i
i ![[x_1, b].](http://upload.wikimedia.org/math/4/7/1/4716ea65a85653bd342d4d66f8bf4c5b.png)
 albo
albo  Cały proces powtarzany jest dla wybranego przedziału.
Cały proces powtarzany jest dla wybranego przedziału.

 punktów
punktów  należących do dziedziny
należących do dziedziny  , dla których znane są wartości
, dla których znane są wartości 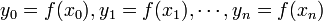
 stopnia co najwyżej
stopnia co najwyżej  takiego, że
takiego, że 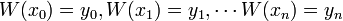 .
. znajduje się wielomian, który w tym punkcie przyjmuje wartość
znajduje się wielomian, który w tym punkcie przyjmuje wartość  wartość zero.
wartość zero.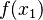 , a w pozostałych węzłach
, a w pozostałych węzłach  wartość zero.
wartość zero.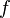 takimi, że znane są wartości
takimi, że znane są wartości 
 ,
, 

 jest
jest  )
) i
i  :
:
 :
:
 )
) będzie wielomianem stopnia co najwyżej
będzie wielomianem stopnia co najwyżej 

 .
. są równe zeru (ponieważ dla
są równe zeru (ponieważ dla  , składnik o indeksie
, składnik o indeksie  .
.
 w punktach
w punktach